何为“二叉搜索树”? 二叉搜索树,是一种特殊的二叉树,你也可以叫他二叉排序树,因为他具有搜索和排序的功能。二叉搜索树的定义很简单:如果在一棵二叉树上,任意结点 $x$ 左子树里的所有点权总是小于 $x$ 的点权,而右子树里的所有点权总是大于 $x$ 的点权,我们就说这棵树是一棵二叉搜索树。比如这个:
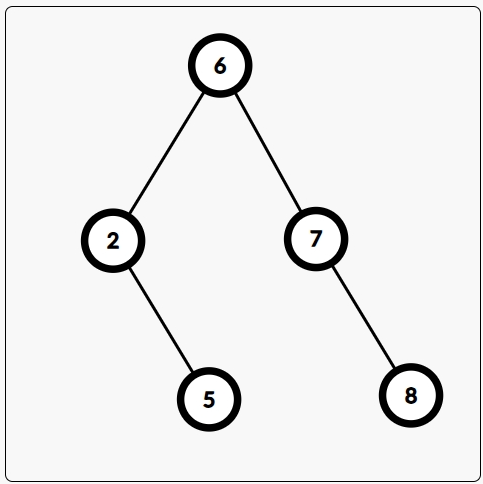
图 1
还有这个:
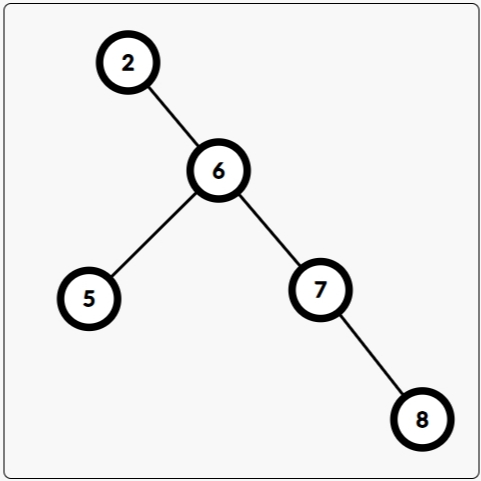
图 2
你可能会发现,两棵二叉树都是二叉搜索树,但上面的看起来均衡一些,也就是平衡一些;而下面的则看起来不太平衡,根节点没有左子树,树的高度也比第一个要高。但是,其实这两棵树对应的序列是一样的,都是 $a=[2,5,6,7,8]$,而二叉搜索树其实就是对应一个序列而生成的,主要目的就是快速维护序列。如果你仔细观察,你可能会发现二叉搜索树的这几个性质:
- 二叉搜索树的中序遍历就是树中所有元素排序后的结果(好神奇!)。
- 我们可以根据二叉搜索树的性质很快地找到某一个元素。比如要找 $5$,我们从根结点出发,如果当前结点的点权小于 $5$,就说明 $5$ 应该在这个结点的右子树里;否则,这个 $5$ 就应该在这个结点的左子树里。根据图 $$ $1$,我们可以发现这一点(建议手动模拟一下!)。删除某个结点也是一样。
- 上述查找和删除结点的操作,时间复杂度是多少呢?这实际上是取决于树的高度的,因为在极限情况下,要查找或删除的结点有可能是一个叶子结点,也就是在树的最底端,此时我们就要经过
重重危险许多结点才能到达叶子结点,而经过的结点数量就是树的高度(想想是不是这样)。 如果是这样,那么如果我们想快速用二叉搜索树维护一个序列,就得保证树的高度尽量小,这样。通过上面的两幅图以及我们的直觉,容易发现二叉树越平衡,树的高度越小。也就是说,我们需要一种办法来让二叉搜索树尽量平衡,这种方法融合进二叉搜索树里就变成了平衡树! 这种维护二叉树平衡的方法有很多种,平衡树的种类也就自然有很多了。我们第一个要学习的平衡树是什么呢?往下看!